Intro
一個解線性聯立方程式 Ax=b 的電路。該電路將A視為一固定矩陣,b為輸入,此電路要將x算出。電路以Finite State Machine設計,配合Gauss-Seidel手法求解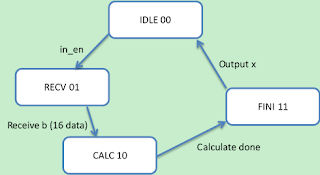
Content

需求是輸入 16-bit integer,輸出 16-bit integer + 16-bit decimal。
為求精準度,我們增加decimal到33-bit,可剛好讓所有testfixture都到達A級。
為了避免溢位造成計算上的不便,我們增加8-bit給integer做表示,亦可增加到16-bit,但為減少Area以8-bit測試可通過。
`timescale 1ns/10ps //`include "timescale.v"
`define mataddr(r, c) r*N + c
`define acrc_ei_w 8 //extension int width
`define acrc_ef_w 33//extension float width
//variable accuracy
module GSIM ( clk, reset, in_en, b_in, out_valid, x_out);
input clk ;
input reset ;
input in_en;
output out_valid;
input [15:0] b_in;
output [31:0] x_out;
parameter N = 16;
parameter STATE_IDLE = 2'b00;
parameter STATE_RECV = 2'b01;
parameter STATE_CALC = 2'b10;
parameter STATE_FINI = 2'b11;
parameter Max_ItTimes = 100;
/*port*/
reg out_valid;
reg [31:0] x_out;
/*internal signal*/
reg [15:0] bv[0:N-1];//b-vector
reg [`acrc_ei_w+15+`acrc_ef_w:0] x0[0:N-1];
reg [`acrc_ei_w+15+`acrc_ef_w:0] x1[0:N-1];
reg [`acrc_ei_w+15+`acrc_ef_w:0] aii_inv;
reg [64:0] aii_inv_def;
reg [31:0] data_times;
reg [31:0] data_times_next;
reg [31:0] it_times;
reg [31:0] it_times_next;
reg [1:0] state;
reg [1:0] state_next;
//reg [15:0] matA[0:N*N-1];
integer i,j;//loop flag
integer idx_init, idx_update;
always @(posedge clk or posedge reset)begin
if( reset ) begin
data_times <= 32'b0;
it_times <= 32'b0;
state <= STATE_IDLE;
for(i=0 ; i < N ; i = i+1)begin
x0[i] <= 0;
end
/*
for(i=0 ; i < N ; i = i+1)begin
//set matrix A
for(j=0 ; j < N ; j = j+1)begin
case( i - j )
0: begin matA[`mataddr(i,j)] <= 20; end//20
1: begin matA[`mataddr(i,j)] <= ~(16'h000d)+1; end//-13
-1: begin matA[`mataddr(i,j)] <= ~(16'h000d)+1; end//-13
2: begin matA[`mataddr(i,j)] <= 6; end//6
-2: begin matA[`mataddr(i,j)] <= 6; end//6
3: begin matA[`mataddr(i,j)] <= ~(16'h0001)+1; end//-1
-3: begin matA[`mataddr(i,j)] <= ~(16'h0001)+1; end//-1
default:begin matA[`mataddr(i,j)] <= 0; end
endcase
end
end*/
aii_inv_def = 64'h0ccc_cccc_cccc_cccc;//64'h0ccc_cccc_cccc_cd00;
aii_inv = {`acrc_ei_w'h0, 16'h0, aii_inv_def[63:64-`acrc_ef_w]};
end else begin
data_times <= data_times_next;
it_times <= it_times_next;
state <= state_next;
for(idx_update=0 ; idx_update < N ; idx_update=idx_update+1)begin
x0[idx_update] <= x1[idx_update];
end
end
end
always @* begin
//for synthesizbility
if(reset)begin
data_times_next = 0;
it_times_next = 32'b0;
state_next = STATE_IDLE;
for(i=0 ; i < N ; i = i+1)begin
bv[i] = 0;
x1[i] = 0;
end
end else begin
case( state )
STATE_IDLE: begin
if(in_en) begin
bv[data_times] = b_in;
data_times_next = data_times + 1;
state_next = STATE_RECV;
end else begin
bv[data_times] = 32'b0;
data_times_next = 32'b0;
state_next = STATE_IDLE;
end
end
STATE_RECV: begin
state_next = STATE_RECV;
if(data_times >= N)begin
state_next = STATE_CALC;
end else if(in_en)begin
bv[data_times] = b_in;
data_times_next = data_times + 1;
end else begin
bv[data_times] = 0;
data_times_next = data_times;
end
end
STATE_CALC: begin
state_next = STATE_CALC;
it_times_next = it_times + 1;
if(it_times == 0)begin
//first loop - initial x
for(idx_init=0 ; idx_init < N ; idx_init=idx_init+1)begin
x1[idx_init] = signed_multiply_int(bv[idx_init], aii_inv);
end
end else if (it_times < Max_ItTimes) begin
$display("===%d===========", it_times);
//iteration loop - update x
x1[0] = signed_multiply(
signed_multiply_int(bv[0], {`acrc_ei_w'h0, 16'h0001, `acrc_ef_w'h0})
//minus x1-partial
//minus x0-partial
+ signed_multiply_int(16'd13, x0[1])
- signed_multiply_int(16'd6, x0[2])
+ x0[3]
, aii_inv)
;
x1[1] = signed_multiply(
signed_multiply_int(bv[1], {`acrc_ei_w'h0, 16'h0001, `acrc_ef_w'h0})
//minus x1-partial
+ signed_multiply_int(16'd13, x1[0])
//minus x0-partial
+ signed_multiply_int(16'd13, x0[2])
- signed_multiply_int(16'd6, x0[3])
+ x0[4]
, aii_inv)
;
x1[2] = signed_multiply(
signed_multiply_int(bv[2], {`acrc_ei_w'h0, 16'h0001, `acrc_ef_w'h0})
//minus x1-partial
- signed_multiply_int(16'd6, x1[0])
+ signed_multiply_int(16'd13, x1[1])
//minus x0-partial
+ signed_multiply_int(16'd13, x0[3])
- signed_multiply_int(16'd6, x0[4])
+ x0[5]
, aii_inv)
;
x1[3] = signed_multiply(
signed_multiply_int(bv[3], {`acrc_ei_w'h0, 16'h0001, `acrc_ef_w'h0})
//minus x1-partial
+ x1[0]
- signed_multiply_int(16'd6, x1[1])
+ signed_multiply_int(16'd13, x1[2])
//minus x0-partial
+ signed_multiply_int(16'd13, x0[4])
- signed_multiply_int(16'd6, x0[5])
+ x0[6]
, aii_inv)
;
x1[4] = signed_multiply(
signed_multiply_int(bv[4], {`acrc_ei_w'h0, 16'h0001, `acrc_ef_w'h0})
//minus x1-partial
+ x1[1]
- signed_multiply_int(16'd6, x1[2])
+ signed_multiply_int(16'd13, x1[3])
//minus x0-partial
+ signed_multiply_int(16'd13, x0[5])
- signed_multiply_int(16'd6, x0[6])
+ x0[7]
, aii_inv)
;
x1[5] = signed_multiply(
signed_multiply_int(bv[5], {`acrc_ei_w'h0, 16'h0001, `acrc_ef_w'h0})
//minus x1-partial
+ x1[2]
- signed_multiply_int(16'd6, x1[3])
+ signed_multiply_int(16'd13, x1[4])
//minus x0-partial
+ signed_multiply_int(16'd13, x0[6])
- signed_multiply_int(16'd6, x0[7])
+ x0[8]
, aii_inv)
;
x1[6] = signed_multiply(
signed_multiply_int(bv[6], {`acrc_ei_w'h0, 16'h0001, `acrc_ef_w'h0})
//minus x1-partial
+ x1[3]
- signed_multiply_int(16'd6, x1[4])
+ signed_multiply_int(16'd13, x1[5])
//minus x0-partial
+ signed_multiply_int(16'd13, x0[7])
- signed_multiply_int(16'd6, x0[8])
+ x0[9]
, aii_inv)
;
x1[7] = signed_multiply(
signed_multiply_int(bv[7], {`acrc_ei_w'h0, 16'h0001, `acrc_ef_w'h0})
//minus x1-partial
+ x1[4]
- signed_multiply_int(16'd6, x1[5])
+ signed_multiply_int(16'd13, x1[6])
//minus x0-partial
+ signed_multiply_int(16'd13, x0[8])
- signed_multiply_int(16'd6, x0[9])
+ x0[10]
, aii_inv)
;
x1[8] = signed_multiply(
signed_multiply_int(bv[8], {`acrc_ei_w'h0, 16'h0001, `acrc_ef_w'h0})
//minus x1-partial
+ x1[5]
- signed_multiply_int(16'd6, x1[6])
+ signed_multiply_int(16'd13, x1[7])
//minus x0-partial
+ signed_multiply_int(16'd13, x0[9])
- signed_multiply_int(16'd6, x0[10])
+ x0[11]
, aii_inv)
;
x1[9] = signed_multiply(
signed_multiply_int(bv[9], {`acrc_ei_w'h0, 16'h0001, `acrc_ef_w'h0})
//minus x1-partial
+ x1[6]
- signed_multiply_int(16'd6, x1[7])
+ signed_multiply_int(16'd13, x1[8])
//minus x0-partial
+ signed_multiply_int(16'd13, x0[10])
- signed_multiply_int(16'd6, x0[11])
+ x0[12]
, aii_inv)
;
x1[10] = signed_multiply(
signed_multiply_int(bv[10], {`acrc_ei_w'h0, 16'h0001, `acrc_ef_w'h0})
//minus x1-partial
+ x1[7]
- signed_multiply_int(16'd6, x1[8])
+ signed_multiply_int(16'd13, x1[9])
//minus x0-partial
+ signed_multiply_int(16'd13, x0[11])
- signed_multiply_int(16'd6, x0[12])
+ x0[13]
, aii_inv)
;
x1[11] = signed_multiply(
signed_multiply_int(bv[11], {`acrc_ei_w'h0, 16'h0001, `acrc_ef_w'h0})
//minus x1-partial
+ x1[8]
- signed_multiply_int(16'd6, x1[9])
+ signed_multiply_int(16'd13, x1[10])
//minus x0-partial
+ signed_multiply_int(16'd13, x0[12])
- signed_multiply_int(16'd6, x0[13])
+ x0[14]
, aii_inv)
;
x1[12] = signed_multiply(
signed_multiply_int(bv[12], {`acrc_ei_w'h0, 16'h0001, `acrc_ef_w'h0})
//minus x1-partial
+ x1[9]
- signed_multiply_int(16'd6, x1[10])
+ signed_multiply_int(16'd13, x1[11])
//minus x0-partial
+ signed_multiply_int(16'd13, x0[13])
- signed_multiply_int(16'd6, x0[14])
+ x0[15]
, aii_inv)
;
x1[13] = signed_multiply(
signed_multiply_int(bv[13], {`acrc_ei_w'h0, 16'h0001, `acrc_ef_w'h0})
//minus x1-partial
+ x1[10]
- signed_multiply_int(16'd6, x1[11])
+ signed_multiply_int(16'd13, x1[12])
//minus x0-partial
+ signed_multiply_int(16'd13, x0[14])
- signed_multiply_int(16'd6, x0[15])
, aii_inv)
;
x1[14] = signed_multiply(
signed_multiply_int(bv[14], {`acrc_ei_w'h0, 16'h0001, `acrc_ef_w'h0})
//minus x1-partial
+ x1[11]
- signed_multiply_int(16'd6, x1[12])
+ signed_multiply_int(16'd13, x1[13])
//minus x0-partial
+ signed_multiply_int(16'd13, x0[15])
, aii_inv)
;
x1[15] = signed_multiply(
signed_multiply_int(bv[15], {`acrc_ei_w'h0, 16'h0001, `acrc_ef_w'h0})
//minus x1-partial
+ x1[12]
- signed_multiply_int(16'd6, x1[13])
+ signed_multiply_int(16'd13, x1[14])
//minus x0-partial
, aii_inv)
;
/*
for(i=0 ; i < N ; i=i+1)begin
x1[i] = signed_multiply_int(bv[i], {`acrc_ei_w'h0, 16'h0001, `acrc_ef_w'h0});
for(j=0 ; j < i ; j=j+1)begin
x1[i] = x1[i] - signed_multiply_int(matA[`mataddr(i, j)], x1[j]);
end
for(j=i+1 ; j < N ; j=j+1)begin
x1[i] = x1[i] - signed_multiply_int(matA[`mataddr(i, j)], x0[j]);
end
x1[i] = signed_multiply(x1[i], aii_inv);
end
*/
end else begin
data_times_next = 0;
state_next = STATE_FINI;
end
end
STATE_FINI: begin
out_valid = 1;
x_out = x0[data_times][15+`acrc_ef_w:16+`acrc_ef_w-32];
data_times_next = data_times + 1;
if(data_times_next >= N)begin
state_next = STATE_IDLE;
end else begin
state_next = STATE_FINI;
end
end
endcase
end
end
function [`acrc_ei_w+15+`acrc_ef_w:0] signed_multiply_int;
input [15:0] a;
input [`acrc_ei_w+15+`acrc_ef_w:0] b;
reg [15:0] a_temp;
reg [`acrc_ei_w+15+`acrc_ef_w:0] multiplicand;
reg [`acrc_ei_w+15+`acrc_ef_w:0] multiplier;
reg [(`acrc_ei_w+16+`acrc_ef_w)*2-1:0] result;
begin
a_temp = ~a+1;
multiplicand = a[15] ? {`acrc_ei_w'h0, a_temp, `acrc_ef_w'b0} : {`acrc_ei_w'b0, a, `acrc_ef_w'b0};
multiplier = b[`acrc_ei_w+15+`acrc_ef_w] ? ~b + 1 : b;
result = multiplicand * multiplier;
signed_multiply_int = a[15] ^ b[`acrc_ei_w+15+`acrc_ef_w]
? ~result[`acrc_ei_w+15+2*`acrc_ef_w:`acrc_ef_w] + 1 : result[`acrc_ei_w+15+2*`acrc_ef_w:`acrc_ef_w];
end
endfunction
function [`acrc_ei_w+15+`acrc_ef_w:0] signed_multiply;
input [`acrc_ei_w+15+`acrc_ef_w:0] a;
input [`acrc_ei_w+15+`acrc_ef_w:0] b;
reg [`acrc_ei_w+15+`acrc_ef_w:0] multiplicand;
reg [`acrc_ei_w+15+`acrc_ef_w:0] multiplier;
reg [(`acrc_ei_w+16+`acrc_ef_w)*2-1:0] result;
begin
multiplicand = a[`acrc_ei_w+15+`acrc_ef_w] ? ~a + 1 : a;
multiplier = b[`acrc_ei_w+15+`acrc_ef_w] ? ~b + 1 : b;
result = multiplicand * multiplier;
signed_multiply = a[`acrc_ei_w+15+`acrc_ef_w] ^ b[`acrc_ei_w+15+`acrc_ef_w]
? ~result[`acrc_ei_w+15+2*`acrc_ef_w:`acrc_ef_w] + 1 : result[`acrc_ei_w+15+2*`acrc_ef_w:`acrc_ef_w];
end
endfunction
/*
function [`acrc_ei_w+15+`acrc_ef_w:0] esay_divider;
input [`acrc_ei_w+15+`acrc_ef_w:0] a;
input [`acrc_ei_w+15+`acrc_ef_w:0] b;
reg [31:0] i;
reg isNegative;
reg [(`acrc_ei_w+16+`acrc_ef_w)*2-1:0] diff;
reg [(`acrc_ei_w+16+`acrc_ef_w)*2-1:0] dividend;
reg [(`acrc_ei_w+16+`acrc_ef_w)*2-1:0] divider;
reg [`acrc_ei_w+15+`acrc_ef_w:0] temp1;
reg [(`acrc_ei_w+16+`acrc_ef_w)*2-1:0] quotient_temp;
reg [`acrc_ei_w+15+`acrc_ef_w:0] quitient;
begin
isNegative = a[`acrc_ei_w+15+`acrc_ef_w] ^ b[`acrc_ei_w+15+`acrc_ef_w];
temp1 = 1'b0;
dividend = a[`acrc_ei_w+15+`acrc_ef_w] ? {1'b0 , ~a+1} : {1'b0, a};
divider = (b[`acrc_ei_w+15+`acrc_ef_w] ? {~b+1, temp1} : {b, temp1}) >> 1;
for(i=0 ; i < (`acrc_ei_w+16+`acrc_ef_w)*2 ; i = i+1)begin
diff = dividend - divider;
quotient_temp = quotient_temp << 1;
if( !diff[(`acrc_ei_w+16+`acrc_ef_w)*2-1] ) begin
dividend = diff;
quotient_temp[0] = 1'd1;
end
divider = divider >> 1;
end
quitient = quotient_temp[(`acrc_ei_w+16)*2 + `acrc_ef_w - 1:(`acrc_ei_w+16)];
esay_divider = isNegative ? ~quitient+1 : quitient;
end
endfunction
*/
endmodule
沒有留言:
張貼留言